Program Metrics

Introduction

The sail on metrics evaluates the agents using two criteria

1. Detecting the instance when novelty was introduced.

2. Reacting and recovering from novelty.

The figure below shows the different points where the metrics are calculated.

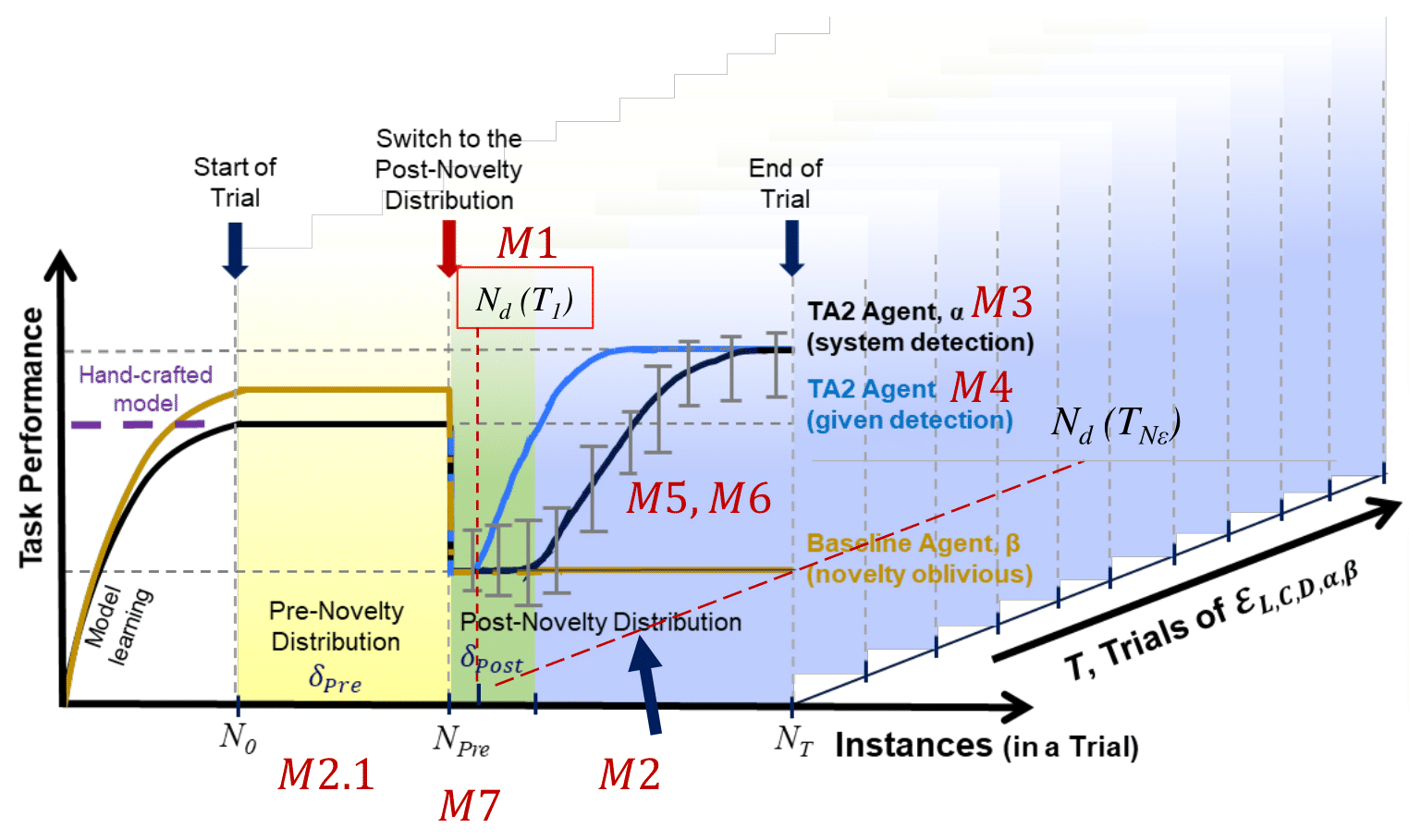
Symbols and Terms

1. L: Novelty Level (L \(\in\) [1,3])

2. C: Condition (C \(\in\) [System Detection, Given Detection])

3. D: Domain (D} \(\in\) [Visual Classification, Document Transcription, Activity Recognition])

4. \(\delta_{pre}\): A distribution of (pre novelty) instances from D at L = 0

5. \(\delta_{post}\): A distribution of (post novelty) instances from D at L \(\geq\) 0

6. \(T_{pre}\): A sequence of instances drawn from \(\delta_{pre}\)

7. \(T_{post}\): A sequence of instances drawn from \(\delta_{post}\)

8. \(T\): A sequence of instances with \(T_{pre}\) and \(T_{post}\)

9. \(\alpha\): A TA2 agent

10. \(\beta\): A Baseline agent

11. \(\mathcal{E}_{L,C,D,\alpha,\beta}\): A set of \(\langle\) L,C, D \(\rangle\) on \(\alpha\) and \(\beta\)

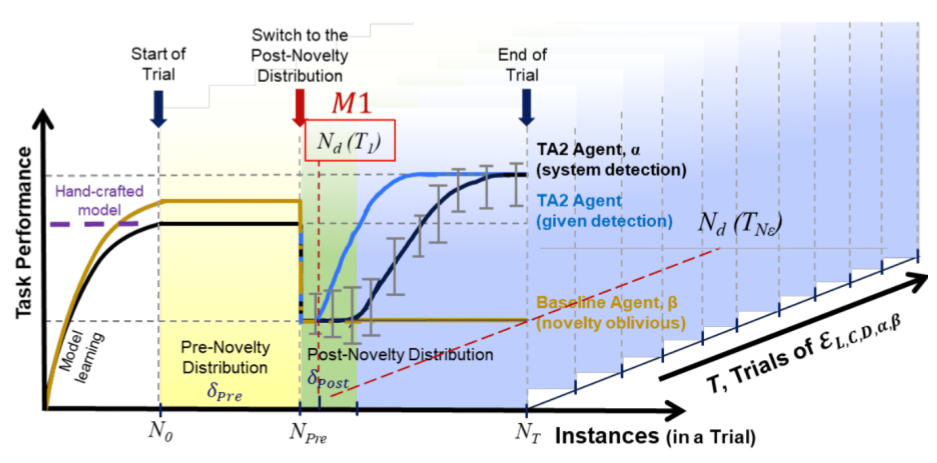
M1: Average Number of FNs among Correctly Detected Trials (⬇ is better)

The goal of the metric is to measure the distance between when novelty was introduced and when the agent declared that the world changed.

Note

M1 is only computed across correctly detected tests.

Formal Definition

Let \(\delta(\alpha, x)\) be the agent’s distribution on instance x

\[\begin{split}CDT(\alpha, T) = \begin{cases} True & \delta_{post}(\alpha, x) \in T_{post} \\ False & \text{otherwise} \end{cases}\end{split}\]

\[\#CDT(\alpha, \mathcal{E}_\alpha) = \sum\limits_{T \in \mathcal{E}_\alpha} CDT(\alpha, T) = \text{True}\]

\[FN(\alpha, T) = \sum\limits_{x \in T_{post}} \delta (\alpha, x) = \delta_{pre}\]

\[\begin{split}\widetilde{FN}_{CDT}(\mathcal{E}_\alpha) = \begin{cases} \frac{1}{\#CDT(\alpha, \mathcal{E}_\alpha)} * \sum\limits_{T \in \mathcal{E}_\alpha \land CDT(\alpha, T)} FN(\alpha, T) & \#CDT(\alpha, \mathcal{E}_\alpha) > 0 \\ \text{N/A} & \text{Otherwise} \end{cases}\end{split}\]

Pictorial Representation

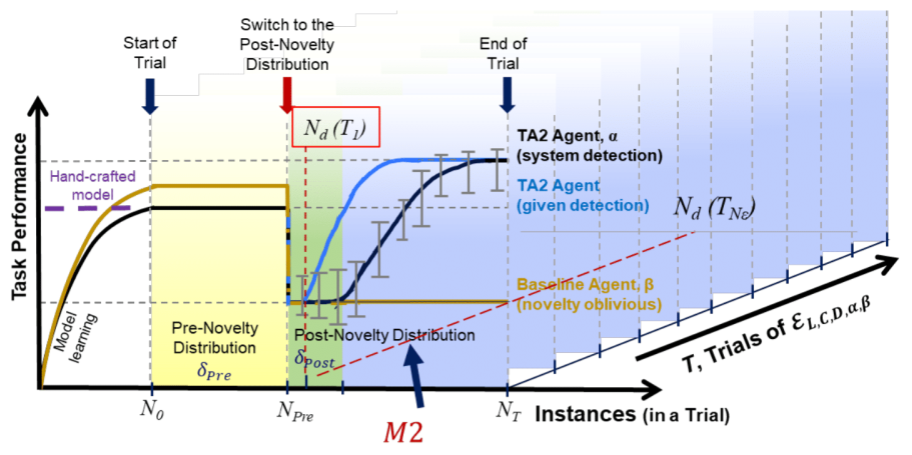
M2: Percentage of Correctly Detected Trials (⬆ is better)

The goal of the metric is to measure the number of tests when agent declares that the world has changed after the novelty is introduced in a test.

Formal Definition

\[CDT_{\%}(\mathcal{E}_\alpha) = \frac{1}{|\mathcal{E}_\alpha|} \sum\limits_{T\in\mathcal{E}_\alpha}(CDT(\alpha, T) = \text{True})\]

Pictorial Representation

M2.1: Percentage of False Positive Trials (⬇ is better)

The goal of the metric is to measure the number of tests when agent declares that the world has changed before the novelty is introduced in a test.

Formal Definition

\[ \begin{align}\begin{aligned}FP(\alpha, T) = \sum\limits_{x \in T_{pre}}(\delta(\alpha, x) = \delta_{post})\\FP_{\%}(\mathcal{E}_\alpha) = \frac{1}{|\mathcal{E}_\alpha|}\sum\limits_{T\in\mathcal{E}_\alpha}(FP(\alpha, T)>0)\end{aligned}\end{align} \]

Pictorial Representation

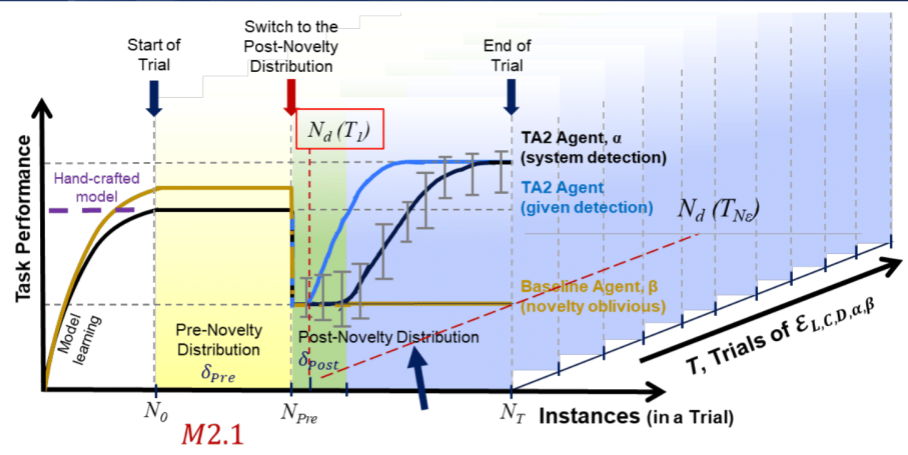
M3 and M4: Novelty Reaction Performance (⬆ is better)

The goal of the metric is to measure the performance of the agent post novelty when compared to a baseline before novelty was introduced. The performance of the agent is measure over asymptotic samples.

Note

The asymptotic samples for a test is the last 100 samples in the test.

Formal Definition

Let \(P_{pre, \beta}\) be baselines average task performance on \(T_{pre}\) and \(P_{post,\alpha}\) be the agents asymptotic task performance on \(T_{post}\)

\[ \begin{align}\begin{aligned}NRP(T) = \frac{P_{post, \alpha}}{P_{pre, \beta}}\\NRP(\mathcal{E}) = \frac{1}{N_\mathcal{E}} \sum\limits_{i=1}^{N_\mathcal{E}} NRP(T_i)\end{aligned}\end{align} \]

Pictorial Representation

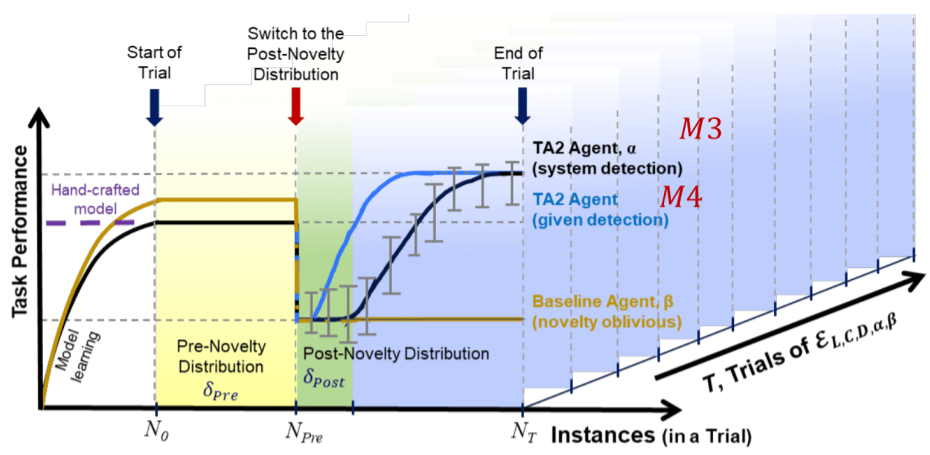
M5: Overall Performance Task Improvement (⬆ is better)

The goal of the metric is to measure the performance of the agent post novelty when compared to the performance of the baseline and the agent post novelty.

Formal Definition

Let \(P_{post, \beta}\) be baselines average task performance on \(T_{post}\) and \(P_{post,\alpha}\) be the agents task performance on \(T_{post}\)

\[ \begin{align}\begin{aligned}OPTI(T) = \frac{P_{post,\alpha}}{P_{post,\alpha} + P_{post, \beta}}\\OPTI = \frac{1}{N_{\mathcal{E}}}\sum\limits_{i=1}^{N_\mathcal{E}}OTPI(T_i)\end{aligned}\end{align} \]

Pictorial Representation

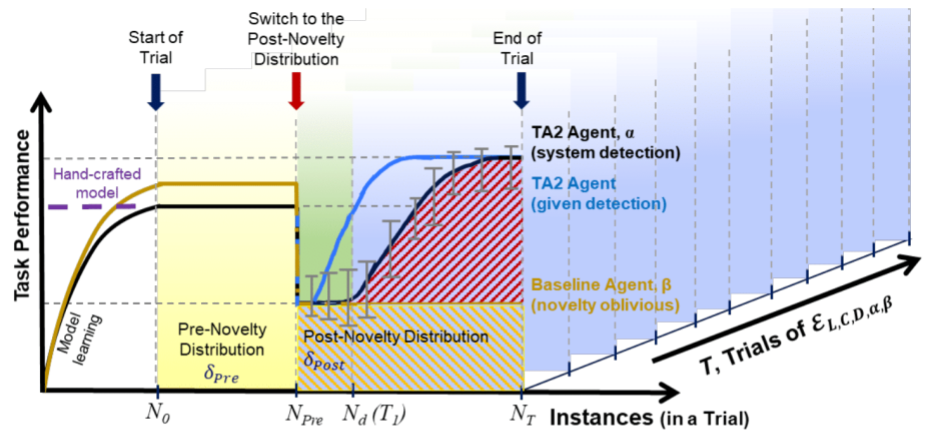
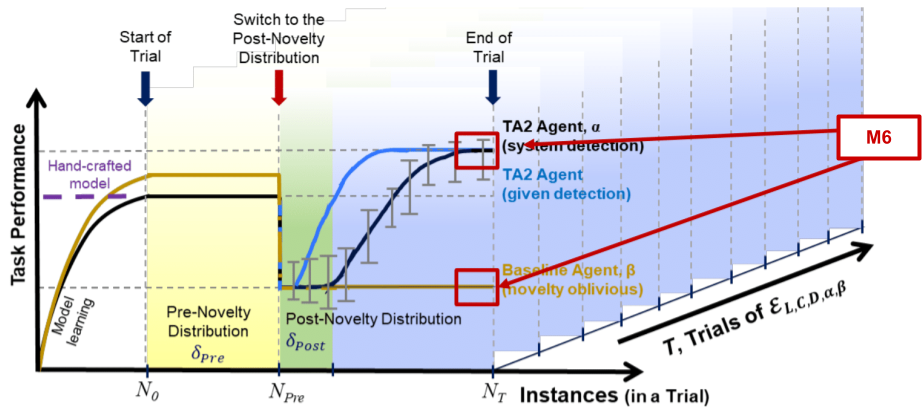
M6: Asymptotic Performance Task Improvement (⬆ is better)

The goal of the metric is to measure the performance of the agent post novelty when compared to the performance of the baseline and the agent post novelty for asymptotic samples.

Note

The asymptotic samples for a test is the last 100 samples in the test.

Formal Definition

\[ \begin{align}\begin{aligned}APTI(T) = \frac{\sum_{i=N_T-m}^{N_T}P_{post,\alpha}}{\sum_{i=N_T-m}^{N_T}P_{post,\beta}}\\APTI = \frac{1}{N_{\mathcal{E}}}\sum\limits_{i=1}^{N_\mathcal{E}}APTI(T_i)\end{aligned}\end{align} \]

where \(m\) is asymptotic width that is domain dependent

Pictorial Representation